Question

DOES ANYONE UNDERSTAND??????????

Answer 1

Yes!
The answer to question 1: functions 3, 4, and 1
The answer to question 2: Function 1
The answer to question 3: Function 2

Answer 2

A). slope less than 4 is of function 1, 2, 3.

B). y intercept closest to 0 is of function 1.

C). greatest y intercept is of function 2.

Explanation:

A). Function 1,

Passes through two points (0, -1) and (1, -2)

Slope of the function =
`(y-y')/(x-x')`

=
`(-2+1)/(1-0)`

=
`(-1)/(1)`

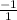
= -1

Function 2,

Passes through two points (-2, 13) and (-1, 9)

Slope of the function =
`(13-9)/(-2+1)`

=
`(4)/(-1)`

= -4

Function 3,

The linear function is y = 3x + 2

Slope of the function = 3

Function 4,

Slope is given as 5.

Therefore, slope less than 4 is of function 1, 2, 3.

B). Function 1.

y intercept of the function = -1

Function 2,

It is given that point (0, 5) lies on the given function.

Therefore, y intercept will be 5.

Function 3,

y = 3x + 2

where y intercept is 2

Function 3,

It is given that y intercept = 2

Therefore, y intercept closest to 0 is of function 1.

C). As we have calculated in part B, greatest y intercept is of function 2.