Question

Two point charges (q1 = -2.5μC and q2 = 7.2 μC) are fixed along the x-axis, separated by a distance d = 9.9 cm. Point P is located at (x,y) = (d,d). Be sure to use a vector approach to answer these problems. It also helps limit the number of calculations since sometimes you can neglect one of the charge's effects due to its location relative to the point in question. 1) What is Ex(P), the value of the x-component of the electric field produced by q1 and q2 at point P? N/C 2) What is Ey(P), the value of the y-component of the electric field produced by q1 and q2 at point P?

Answer 1

To find Ex(P) at point P, calculate the contributions from both charges using Coulomb's law and sum the x-components of the electric fields.

Step-by-step explanation:

To find the x-component of the electric field at point P, we need to calculate the contributions from both charges. The electric field due to q1 can be calculated using Coulomb's law:

E1 = k*(q1/r1^2), where k is the electrostatic constant, q1 is the charge of q1, and r1 is the distance between q1 and P. Similarly, the electric field due to q2 can be calculated:

E2 = k*(q2/r2^2), where q2 is the charge of q2 and r2 is the distance between q2 and P. Finally, the x-component of the electric field at P is the sum of the x-components of E1 and E2:

Ex(P) = E1x + E2x

Answer 2

Epx = -0.81*10⁶ N/C

Epy = 5.79*10⁶ N/C

Step-by-step explanation:

Electric field theory

The electric field at a point P due to a point charge is calculated as follows:

E = k*q/r²

E: Electric field in N/C

q: charge in Newtons (N)

k: electric constant in N*m²/C²

r: distance from load q to point P in meters (m)

The electric field at a point P due to several point charges is the vector sum of the electric field due to individual charges.

Equivalences

1µC= 10⁻⁶ C

1cm= 10⁻² m

Graphic attached

The attached graph shows the field due to the charges:

Ep₁: Total field at point P due to charge q₁. As the charge is negative, the field enters the charge.

Ep₂: Total field at point P due to charge q₂. As the charge is positive ,the field leaves the charge.

Known data

q₁ = -2.5 µC = -2.5*10⁻⁶ C

q₂ = 7,2 µC = 7,2*10⁻⁶ C

k = 8.99*10⁹ N*m²/C²

d = 9.9cm = 9.9*10⁻² m

θ = 45°

sinθ = cosθ =
`(√(2) )/(2)`

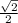
r calculation

`r=\sqrt{(9.9*10^(-2))^2+(9.9*10^(-2))^2}=0.14m`

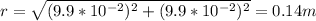
Calculation of the electric field at point P due to q₁

Ep1x = (-k*q₁*cosθ)/r²

`Ep_(1x)= -(8.99*10^9*2.5*10^(-6)(√(2))/(2))/(0.14^2)=-0.81*10^6 (N)/(C)`

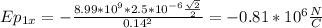
Ep1y = (-k*q₁*sinθ)/r²

`Ep_(1y)= -(8.99*10^9*2.5*10^(-6)(√(2))/(2))/(0.14^2)=-0.81*10^6 (N)/(C)`

Calculation of the electric field at point P due to q₂

Ep2x=0

Ep2y=k*q₁/r²=(8.99*10⁹*7.2 *10⁻⁶)/

(9.9*10⁻²)² = 6.6*10⁶ N/C

Calculation of the electric field at point P due to q₁ and q₂

Epx = Ep1x + Ep2x = -0.81*10⁶ + 0 = -0.81*10⁶ N/C

Epy = Ep1y+ Ep2y= -0.81*10⁶ + 6.6*10⁶ = 5.79*10⁶ N/C