Answer: n=4
Step-by-step explanation:
We have the following expression for the volume flow rate
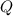 of a hypodermic needle:
of a hypodermic needle:
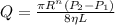 (1)
(1)
Where the dimensions of each one is:
Volume flow rate
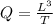
Radius of the needle
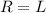
Length of the needle
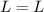
Pressures at opposite ends of the needle
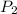 and
and
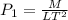
Viscosity of the liquid

We need to find the value of
 whicha has no dimensions, and in order to do this, we have to rewritte (1) with its dimensions:
whicha has no dimensions, and in order to do this, we have to rewritte (1) with its dimensions:
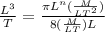 (2)
(2)
We need the right side of the equation to be equal to the left side of the equation (in dimensions):
 (3)
(3)
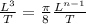 (4)
(4)
As we can see
 must be 4 if we want the exponent to be 3:
must be 4 if we want the exponent to be 3:
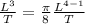 (5)
(5)
Finally:
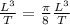 (6)
(6)