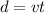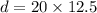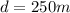Question

At the instant the traffic light turns green, a car that has been waiting at the intersection starts ahead with a constant acceleration of 3.20 m/s^2. At the same instant a truck, travelling with a constant speed of 20.0m/s, overtakes and passes the car. How far beyond its starting point, in metres, does the car overtake the truck?

Please explain your answer and formula used.

Answer 1

d = 250 m

Step-by-step explanation:

As we know that car starts from rest while truck is moving at constant speed

so let say after time t they both passes through the same point

so we have

`d_(truck) = d_(car)`

`20 t = (1)/(2)(3.20) t^2`

`20t = 1.6 t^2`

`t = (20)/(1.6)`

`t = 12.5 s`

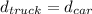
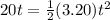
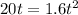
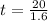
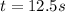
so the distance moved by the truck or the car in the above time is given as

`d = vt`

`d = 20* 12.5`

`d = 250 m`