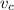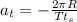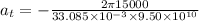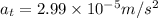Answer:
(a)
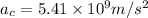
(b)
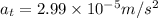
Given:
Time period of Pulsar,
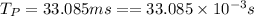
Equatorial radius, R = 15 Km = 15000 m
Spinning time,

Solution:
(a) To calculate the value of the centripetal acceleration,
 on the surface of the equator, the force acting is given by the centripetal force:
on the surface of the equator, the force acting is given by the centripetal force:
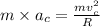
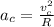 (1)
(1)
where
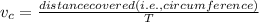
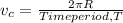 (2)
(2)
Now, from (1) and (2):


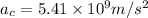
(b) To calculate the tangential acceleration of the object :
The tangential acceleration of the object will remain constant and is given by the equation of motion as:
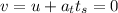
where
u =