Question

Which is an exponential decay function? f start bracket x end bracket equals Three-fourths start bracket Seven-fourths end bracket superscript x f start bracket x end bracket equals two-third start bracket Four-fifths end bracket superscript negative x f start bracket x end bracket equals Three-halves start bracket Eight-sevenths end bracket superscript negative x f start bracket x end bracket equals one-third start bracket negative nine-halves end bracket superscript x

Answer 1

The exponential decay function is
`f(x)=(3)/(2)((8)/(7))^(-x)` ⇒ 3rd answer

Explanation:

* Lets explain the exponential decay function

- The general form of an exponential Function is
`f(x)=a(b)^(x)`,

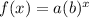where a is the initial value and b is growth factor

- If b > 1 , then the function is exponential growth function

- If 0 < b < 1 , then the function is exponential decay function

- The function
`f(x) = a(b)^(-x)` can be written as

`f(x)=a((1)/(b))^(x)`

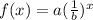
# Remember: if 0 < b < 1 , then 1/b > 1 , then change the negative

sign of the power by reciprocal the growth factor to decide the

function is growth or decay

* Lets solve the problem

1.
`f(x)=(3)/(4)((7)/(4))^(x)`

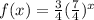
∵ b = 7/4

∵ 7/4 is greater than 1

∴ f(x) is an exponential growth function

2.
`f(x)=(2)/(3)((4)/(5))^(-x)`

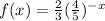
- Change the (-x) to x by reciprocal (4/5) to (5/4)

∴
`f(x)=(2)/(3)((5)/(4))^(x)`

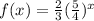
∵ b = 5/4

∵ 5/4 is greater than 1

∴ f(x) is an exponential growth function

3.
`f(x)=(3)/(2)((8)/(7))^(-x)`

- Change the (-x) to x by reciprocal (8/7) to (7/8)

∴
`f(x)=(3)/(2)((7)/(8))^(x)`

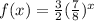
∵ b = 7/8

∵ 7/8 is greater than 0 and smaller than 1 ⇒ 0 < 7/8 < 1

∴ f(x) is an exponential decay function

* The exponential decay function is
`f(x)=(3)/(2)((8)/(7))^(-x)`

Answer 2

The third option, which can be rewritten as:

f(x) = (3/2)*(7/8)ˣ

Which is an exponential decay?

An exponential equation is:

y = a*bˣ

if b > 1, this is an exponential growht.

if 0 < b < 1, this is an exponential decay.

From this, we can see that the correct option is:

" f start bracket x end bracket equals Three-halves start bracket Eight-sevenths end bracket superscript negative x "

or

f(x) = (3/2)*(8/7)⁻ˣ

The negative sign in the exponent means that we need to take the inverse, so we get:

f(x) = (3/2)*(7/8)ˣ