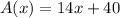Question

A rectangle is (x+10)ft by (x+4)ft. If a square of length xft on a side is cut from the rectangle, represent the remaining area in the form of a polynomial function A(x)

Answer 1

Answer:
`A(x)=14x+40`

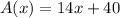
Explanation:

Given : The dimension of a rectangle is (x+10)ft. by (x+4)ft.

Then, Area of rectangle will be :-

`A_1(x)=(x+10)*(x+4)=x^2+(10+4)x+40\\\\\Rightarrow\ A_1(x)=x^2+14x+40`

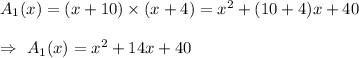
If a square of length xft on a side is cut from the rectangle, then the area of the square :-

`A_2(x)=x^2`

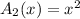
Now, the remaining area in the form of a polynomial function A(x) will be :-

`A(x)=A_1(x)-A_2(x)\\\\=x^2+14x+40-x^2=14x+40`

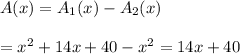
Hence, the remaining area in the form of a polynomial function A(x) will be :-

`A(x)=14x+40`