Question

Is it possible to create a visual model (stop motion) of a wave motion using the differential equation for simple harmonic oscillation and how so?

Answer 1

• Yes.

Step-by-step explanation:

A particular solution for the 1D wave equation has the form

`\Psi(x,t) \ = \ A \ sin ( \ k x \ + \omega t \ + \phi \ )`

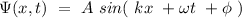
where A its the amplitude, k the wavenumber, ω the angular frequency and φ the phase angle.

Now, for any given position
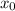`x_0`, we can use:

`\phi_0 \ = \ \phi \ + \ k x_0`

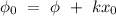
so, the equation its:

`\Psi(x_0,t) \ = \ A \ sin ( \omega t \ + \ \phi_0 )`.

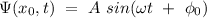This is the equation for a simple harmonic oscillation!

So, for any given point, we can use a simple harmonic oscillation as visual model. Now, when we move a
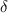`\delta` distance from the original position, we got:

`x_1 = x_0 + \delta`

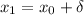
and

`\phi_1 = \phi  \ + k x_1`

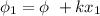
now, this its

`\phi_1 = \phi  \ + k ( x_0 + \delta)`

`\phi_1 = \phi  \ + k  x_0 + k \delta`

`\phi_1 = \phi_0 + k \delta`

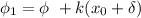
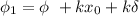
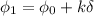
So, there its a phase angle difference of
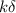`k \delta`. We can model this simply by starting the simple harmonic oscillation with a different phase angle.