Question

A red laser (740 nm) shines on a double slit (slit separation = 0.165 mm). What is the angle of the fourth order maximum (that is, the fourth bright fringe away from the central maximum)?

Answer 1

The angle of the fourth order maximum is 1.027 degrees.

Step-by-step explanation:

It is given that,

Wavelength of red laser,
`\lambda=740\ nm=740* 10^(-9)\ m`

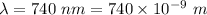
Slit separation,
`d=0.165\ mm= 0.000165\ m`

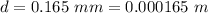
We need to find the angle of the fourth order maximum. For maximum, the equation is given by :

`d\ sin\theta=n\lambda`

`sin\theta=(n\lambda)/(d)`

`sin\theta=(4* 740* 10^(-9))/(0.000165)`

`\theta=1.027^(\circ)`

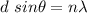
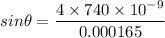
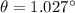
So, the angle of the fourth order maximum is 1.027 degrees. Hence, this is the required solution.