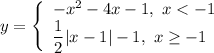Question

Complete a piecewise function that describes the graph.

Answer 1

`y=\left \{ \begin{array}{l}-x^2-4x-1,\ x<-1 \\ (1)/(2)|x-1|-1,\ x\ge -1\end{array} \right.`

Explanation:

Left part of the graph is the graph of the parabola passing through the points (-2,3), (-3,2) and (-4,-1). If the equation of the parabola is
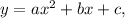`y=ax^2+bx+c,` then

`3=a\cdot (-2)^2+b\cdot (-2)+c\Rightarrow 3=4a-2b+c\\ \\2=a\cdot (-3)^2+b\cdot (-3)+c\Rightarrow 2=9a-3b+c\\ \\-1=a\cdot (-4)^2+b\cdot (-4)+c\Rightarrow -1=16a-4b+c`

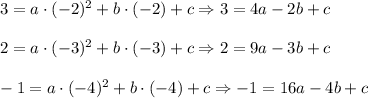
Subtract first two equations and last two equations:

`-1=5a-b\\ \\-3=7a-b`

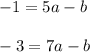
Suybtract these two equations:

`-2=2a\Rightarrow a=-1`

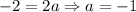
So
`-1=5\cdot (-1)-b\Rightarrow b=-5+1=-4`

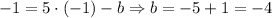
Substitute into the first equation:

`3=4\cdot (-1)-2\cdot (-4)+c\Rightarrow c=3+4-8=-1`

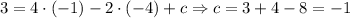
The equation of the parabola is
`y=-x^2-4x-1`

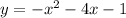
The right part of the graph is translated 1 unit to the right and 1 unit down graph of the function
`y=(1)/(2)|x|`, so it has the equation
`y=(1)/(2)|x-1|-1`

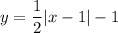
Hence, the piece-wise function is

`y=\left \{ \begin{array}{l}-x^2-4x-1,\ x<-1 \\ (1)/(2)|x-1|-1,\ x\ge -1\end{array} \right.`