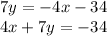Question

Find an equation of the line passing through the points (−5,−2) with the slope m= -( 4/7)

Answer 1

The equation in point slope form is
`y+2=-(4)/(7)(x+5)`

The equation in slope intercept form is
`y=-(4)/(7)x-(34)/(7)`

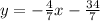
The equation in standard form is
`4x+7y=-34`

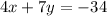
Explanation:

we know that

The equation of the line in point slope form is equal to

`y-y1=m(x-x1)`

we have

`m=-(4)/(7)`

`point\ (-5,-2)`

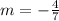
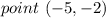
substitute

`y+2=-(4)/(7)(x+5)` ----> equation of the line in point slope form

Convert to slope intercept form

`y=mx+b`

`y+2=-(4)/(7)x-(20)/(7)`

`y=-(4)/(7)x-(20)/(7)-2`

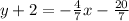
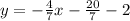
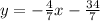`y=-(4)/(7)x-(34)/(7)` ----> slope intercept form

Convert to standard form

`Ax+By=C`

where

A is a positive integer

B and C are integer

`y=-(4)/(7)x-(34)/(7)`

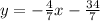
Multiply by 7 both sides to remove the fraction

`7y=-4x-34\\4x+7y=-34`