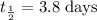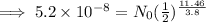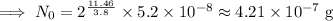Answer:
(i) Approximately 3 half lifes
(ii)
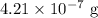
Explanation:
(i) ∵ The half life of Radon-222 is approximately 3.8 days,
So, the number of half life in 11.46 days =
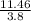 ≈ 3
≈ 3
(ii) Since, the half life formula is,
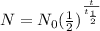
Where,
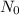 = initial quantity,
= initial quantity,
t = number of periods
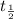 = half life of the quantity,
= half life of the quantity,
Given,
N =
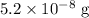
t = 11.46 days,