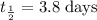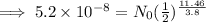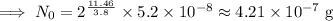Question

How many half-lives of radon-222 have passed in 11.46 days? If 5.2 × 10−8 g of radon-222 remain in a sealed box after 11.46 days, how much was present in the box initially socratic.org

Answer 1

(i) Approximately 3 half lifes

(ii)
`4.21* 10^(-7)\text{ g}`

Explanation:

(i) ∵ The half life of Radon-222 is approximately 3.8 days,

So, the number of half life in 11.46 days =
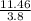`(11.46)/(3.8)` ≈ 3

(ii) Since, the half life formula is,

`N=N_0 ((1)/(2))^{\frac{t}{t_{(1)/(2)}}}`

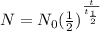
Where,

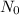`N_0` = initial quantity,

t = number of periods

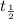`t_{(1)/(2)}` = half life of the quantity,

Given,

N =
`5.2* 10^(-8)\text{ g}`

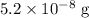
t = 11.46 days,

`t_{(1)/(2)} = 3.8\text{ days}`

`\implies 5.2* 10^(-8)=N_0 ((1)/(2))^(11.46)/(3.8)`

`\implies N_0=2^{(11.46)/(3.8)}* 5.2* 10^(-8)\approx 4.21* 10^(-7)\text{ g}`