Question

A gondola on an amusement park ride spins at a speed of 14 revolutions per minute. If the gondola is 24 feet from the​ ride's center, what is the linear speed of the gondola in miles per​ hour?

Answer 1

The linear speed of the gondola is 23.99 mils/hr.

Step-by-step explanation:

Given that,

Number = 14 revolution /m

Distance = 24 feet

We need to calculate the linear speed of the gondola in miles per​ hour

Using formula of speed

`v = r\omega`

`v=(r2\pi N)/(60)`

Put the value into the formula

`v=(24*2*\pi*14)/(60)`

`v=35.18\ ft/s`

`v=23.99\ mile/hr`

Hence, The linear speed of the gondola is 23.99 mils/hr.

Answer 2

Linear speed, v = 23.86 miles per hour

Step-by-step explanation:

It is given that,

Angular speed of gondola,
`\omega=14\ rev/min=1.46\ rad/sec`

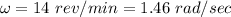
The gondola is 24 feet from the​ ride's center, r = 24 feet = 7.31 m

We need to find the linear speed of the gondola. It can be calculated using the following relation as :

`v=r* \omega`

`v=7.31\ m* 1.46\ rad/s`

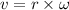
v = 10.67 m/s

or

v = 23.86 miles per hour

So, the linear speed of the gondola is 23.86 miles per hour. Hence, this is the required solution.