Question

Form a polynomial whose zeros and degree are given. ​Zeros: negative 4​, multiplicity​ 1; negative 3​, multiplicity​ 2; degree 3

Answer 1

Required polynomial is

`P(x)=a(x+4)(x+3)^2`

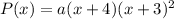
where, a can be any real number.

Explanation:

The factored form of a polynomial is

`P(x)=a(x-c_1)^(m_1)(x-c_2)^(m_2)...(x-c_n)^(m_n)`

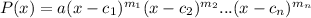
where, a is constant,
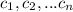`c_1,c_2,...c_n` are zeroes with multiplicity
`m_1,m_2,...,m_n` respectively.

It is given that -4 is a zero of required polynomial with multiplicity​ 1. It means
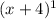`(x+4)^1` is a factor of required polynomial.

It is given that -3 is a zero of required polynomial with multiplicity​ 2. It means
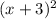`(x+3)^2` is a factor of required polynomial.

Required polynomial is

`P(x)=a(x+4)(x+3)^2`

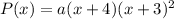
where, a can be any real number.