Question

Two spheres are tangent to each other. One has a volume of 36π, and the other has a volume of 288π. What is the greatest distance between a point on one of the spheres and a point on the other sphe

Answer 1

18 m

Step-by-step explanation:

In the given figure we have two sphere one has volume
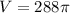`V=288\pi` and other has volume
`V=36\pi`

The greatest distance between the one point of the sphere to other sphere will be the sum of diameter of both sphere

We know that volume of the sphere
`V=(4)/(3)\pi r^3`

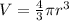
So for larger sphere
`288\pi =(4)/(3)\pi r^3`

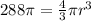
r = 6 m, so diameter d =6×2=12 m

Now for smaller sphere
`36\pi  =(4)/(3)\pi r^3`

r = 3 m , so diameter d=3×2=6 m

So the greatest distance between two sphere is 6+12=18 m