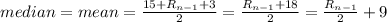Question

The first term of set R is 15. What is the median value of the set R, if for every term in the set, Rn = Rn–1 + 3?

Answer 1

`median=mean=(R_(n-1))/(2)+9`

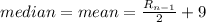
Explanation:

The first thing to identify is that this one is a consecutive set, meaning that the increment between each number is the same, in this case, an increment of 3 between each number, when sets have this type of behavior, and only on these cases, the mean and the median are the same, let's look at some examples:

[2, 4, 6, 8, 10, 12]

The mean would be:

mean=
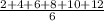`(2+4+6+8+10+12)/(6)`=7

Since the number of elements is even, the median would be the average of the two middle terms:

median=
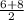`(6+8)/(2)`=7

As you can see mean=median

There is one more thing to help you in this exercise, for consecutive sets, the mean can also be calculated by the formula:

`mean=(x_(1) + x_(n) )/(2)`

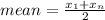
Where
`x_(1)` is the first term of the set and
`x_(n)` is the last.

If we ran this formula with the set i used as an example:

mean=
`(2+12)/(2)=7`.

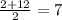So applying all of that to the set given we would have:

`median=mean=(15+R_(n-1)+3)/(2) =(R_(n-1)+18)/(2) =(R_(n-1))/(2)+9`