Question

Zach and Warren both leave the coffee shop at the same time, but in opposite directions. If Warren travels 7 mph faster than Zach and after 7 hours they are 161 miles apart, how fast is each traveling?

Answer 1

Answer: Speed of Zach = 16 mph

Sspeed of Warren = 16+7=23 mph

Explanation:

Let x be the speed of Zach in mph , the speed of Warren will be x+7 mph.

Formula to find distance :-

`\text{Distance=Speed * Time}`

Then, distance covered by Zach in 7 hours =
`x* 7=7x`

Distance covered by Warren =
`7(x+7)`

Then, according to the question, we have

`7(x+7)=161\\\\\Rightarrow\ x+7=23\\\\\Rightarrow\ x=23-7=16`

Hence, the speed of Zach = 16 mph

The speed of Warren = 16+7=23 mph

Answer 2

The speed of the Zach travelling is 8 miles per hour.

The speed of the Warren travelling is 15 miles per hour.

Explanation:

Given : Zach and Warren both leave the coffee shop at the same time, but in opposite directions. If Warren travels 7 mph faster than Zach and after 7 hours they are 161 miles apart.

To find : How fast is each traveling?

Solution :

Let the speed of Zach is x mile per hour.

If Warren travels 7 mph faster than Zach

The speed of the Warren is x+7 miles per hour.

Zach and Warren both leave the coffee shop at the same time, but in opposite directions.

The distance covered is 161 miles in 7 hours.

We know,
`\text{Distnace}=\text{Speed}* \text{Time}`

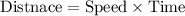
Substitute,

`161=(x+x+7)*7`

`(161)/(7)=2x+7`

`23=2x+7`

`2x=23-7`

`2x=16`

`x=8`

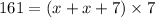
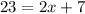
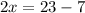
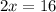
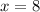
The speed of Warren is 8+7=15

The speed of the Zach travelling is 8 miles per hour.

The speed of the Warren travelling is 15 miles per hour.