Question

Saturn moves in an orbit around the Sun with radius 10 AU. How many degrees does it move on the Celestial in one year? (Hint: Calculate its orbital period). A. About I degree B. About 12 degrees C About 30 degrees D. About 90 degrees E. 360 degroes

Answer 1

B. About 12 degrees

Step-by-step explanation:

The orbital period is calculated using the following expression:

T = 2π*(
`\sqrt{(r^3)/(Gm)}`)

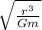Where r is the distance of the planet to the sun, G is the gravitational constant and m is the mass of the sun.

Now, we don't actually need to solve the values of the constants, since we now that the distance from the sun to Saturn is 10 times the distance from the sun to the earth. We now this because 1 AU is the distance from the earth to the sun.

Now, we divide the expression used to calculate the orbital period of Saturn by the expression used to calculate the orbital period of the earth. Notice that the constants will cancel and we will get the rate of orbital periods in terms of the distances to the sun:

`(Tsaturn)/(Tearth)` =
`\sqrt{(rSaturn^3)/(rEarth^3) } = √(10^3)}`

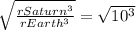
Knowing that the orbital period of the earth is 1 year, the orbital period of Saturn will be
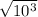`√(10^3)}` years, or 31.62 years.

We find the amount of degrees it moves in 1 year:

`1year * (360degrees)/(31.62years) = 11.38 degrees`

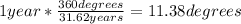
or about 12 degrees.