Question

If a vector A has components A. 0, and Ay -0, then the magnitude of the vector is negative. Select one: True False

Answer 1

The given statement is false.

Step-by-step explanation:

For a given vector
`\overrightarrow{A}=A_(x)\widehat{i}+A_(y)\widehat{j}`

The magnitude is given by
`|A|=\sqrt{A_(x)^(2)+A_(y)^(2)}`

As we can see that the quantity on the right side of equation is always positive since square root of a quantity is always positive thus we conclude that the magnitude of any vector and hence vector A is always positive.

Answer 2

False

Step-by-step explanation:

The magnitude of any vector is given by,

`||A||=√(A_x^2+A_y^2)`

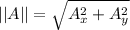
The magnitude of anything is never negative. It can be even seen from the formula that the components are squared. A squared value can never be negative. Even if the component is negative the square will be always positive.

So, magnitude of the vector is not negative.