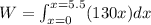Answer:
Part a)
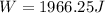
Part b)
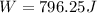
Part c)
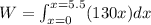
Step-by-step explanation:
Part a)
As we know that 65 N force is required to pull the spring by x = 0.5 m
so we will have
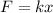
here we know that
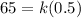
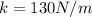
now we need to find the work to stretch it by 5.5 m from equilibrium position
So it is given as
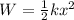
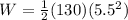
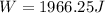
Part b)
Work done to compress the spring by 3.5 m is given as
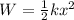
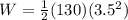
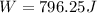
Part c)
Work done by variable force is given as
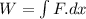
so here we need to stretch it from x = 0 to x = 5.5
so we will have
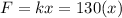
now work done is given as