Question

Each participant in a certain study was assigned a sequence of 3 different letters from the set {A, B, C, D, E, F, G, H}. If no sequence was assigned to more than one participant and if 36 of the possible sequences were not assigned, what was the number of participants in the study? (Note, for example, that the sequence A, B, C is different from the sequence C, B, A.)A 20B 92C 300D 372E 476

Answer 1

C:300

Explanation:

We are given that each participants in a certain study was assigned a sequence of 3 different letters from the set {A,B,C,D,E,F,G,H}

Number of letters =n=8

We are given that number of possible sequence were not assigned =36

We are given that no sequence was assigned to more than one participant.

We have to find that number of participants in the study

Permutation formula :
`nP_r=(n!)/((n-r)!)`

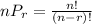
We have r=3

Using the permutation formula

The number of sequence were assigned =
`8P_3=(8!)/((8-3)!)`

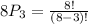
The number of sequence were assigned =
`(8* 7* 6* 5!)/(5!)`

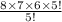
The number of sequence were assigned =336

But we are given that 36 of possible sequence were not assigned

Therefore, required number of sequence were assigned=336-36=300

Number of sequence assigned=Number of participants

Therefore, number of participants in the study=300

Answer:C:300