Question

A 2 x106 kg rocket is launched from the surface of the Earth What is the escape speed in km/s) of the rocket with respect to its gravitational interaction with the Sun? The intial distance of the rocket from the Sun s 150 x1o!1m and the mass of the Sun is 1.99 x 1030 kg You may ignoreal other gravitational ntoractions for the rocket and assume r gravitational interactions for the rocket and assume that the system is isolated

Answer 1

Escape speed of the rocket, v = 4206.86 m/s

Step-by-step explanation:

Mass of the rocket,
`m=2* 10^6\ kg`

We need to find the escape speed of the rocket with respect to its gravitational interaction with the Sun. It is given by :

`v=\sqrt{(2GM)/(R)}`

Where

G is the universal gravitational constant

R is the distance

`v=\sqrt{(2* 6.67* 10^(-11)* 1.99* 10^(30))/(150* 10^(11))}`

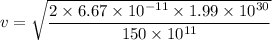
v = 4206.86 m/s

So, the escape speed of the rocket is 4206.86 m/s. Hence, this is the required solution.