Question

Given the initial wavefunction Ψ (x, 0) = Axexp (-k x) withx> 0 andk> 0, and Ψ (x, 0) = 0 forx <0, what value must A take in terms ofkin order that Ψ is normalized? Find , , and σ.

Answer 1

Answer with explanation:

The Normalization Principle states that

`\int_(-\infty )^(+\infty )f(x)dx=1`

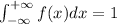
Given

`f(x)=xe^(-kx)(x>0\\\\0(x<0)`

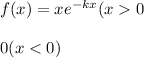
Thus solving the integral we get

`\int_(0 )^(+\infty )A\cdot xe^(-kx)dx=1\\\\A\int_(0 )^(+\infty )\cdot xe^(-kx)dx=1`

The integral shall be solved using chain rule initially and finally we shall apply the limits as shown below

`I=\int xe^(-kx)dx\\\\x\int e^(-kx)dx-\int (d(x))/(dx)\int e^(-kx)dx\\\\-(xe^(-kx))/(k)-\int 1\cdot (-e^(-kx))/(k)\\\\\therefore I=(e^(-kx))/(k)-(xe^(-kx))/(k)`

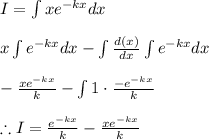
Applying the limits and solving for A we get

`I=(1)/(k)[(1)/(e^(kx))-(x)/(e^(kx))]_(0)^(+\infty )\\\\I=-(1)/(k)\\\\\therefore A=-k`