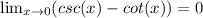Answer with Step-by-step explanation:
We are given that

We have to prove that why the limit x approaches 0(csc(x)-cot(x)) involves an indeterminate form and prove that the limit equals to 0.
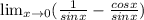
Because
 and
and
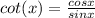
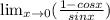
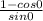
We know that cos 0=1 and sin 0=0
Substitute the values then we get
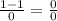
We know that
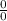 is indeterminate form
is indeterminate form
Hence, the limit x approaches 0(csc(x)-cot(x)) involves an indeterminate form.
L'hospital rule:Apply this rule and differentiate numerator and denominator separately when after applying
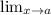 we get indeterminate form
we get indeterminate form
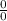
Now,using L' hospital rule
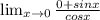
because
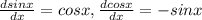
Now, we get

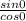
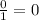
Hence,