Question

Find magnetic field at the center of flat coil of insulated current carrying wire, I, where radius of infinite coil relates to r = a(1+theta^2).

Answer 1

The magnetic field at the center of flat coil is
`(\mu_(0)I)/(8a)`.

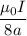Step-by-step explanation:

Given that,

Radius
`r = a(1+\theta^2)`

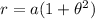
We need to calculate the magnetic field at the center of flat coil

Using Biot-savart law

`dB=(\mu_(0)Idl\sin\alpha)/(4\pi* r^2)`

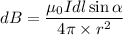
Here,
`\alpha =90^(/circ)`

`dl=rd\theta`

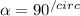
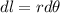
Then, the magnetic field

`dB=(\mu_(0)Ird\theta\sin90)/(4\pi* r^2)`

`dB=(\mu_(0)Id\theta)/(4\pi* r)`

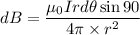
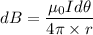
Put the value of r

`dB=(\mu_(0)Id\theta)/(4\pi* a(1+\theta^2))`

`dB=(\mu_(0)I)/(4\pi a)\int_(0)^(\infty){(d\theta)/((1+\theta^2))}`

`dB=(\mu_(0)I)/(4\pi a)(1(\tan^2\theta))_(0)^(\infty)`

`dB=(\mu_(0)I)/(4\pi a)((\pi)/(2)-0)`

`dB=(\mu_(0)I)/(4\pi a)*(\pi)/(2)`

`dB=(\mu_(0)I)/(8a)`

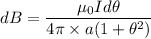
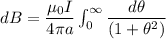
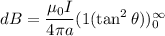
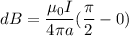
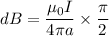
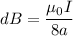
Hence, The magnetic field at the center of flat coil is
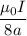`(\mu_(0)I)/(8a)`.