Answer:
Explanation:
We are given that G be a finite group with
 have two elements of order two.
have two elements of order two.
We have to prove that <x,y> is either abelian or isomorphic to a dihedral group.
<x,y> means the group generated by two elements of order 2.
We know that
 is a cyclic group and number of elements of order 2 is always odd in number and generated by one element .So , given group is not isomorphic to
is a cyclic group and number of elements of order 2 is always odd in number and generated by one element .So , given group is not isomorphic to
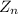
But we are given that two elements of order 2 in given group
Therefore, group G can be
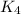 or dihedral group
or dihedral group
Because the groups generated by two elements of order 2 are
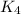 and dihedral group.
and dihedral group.
We know that
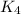 is abelian group of order 4 and every element of
is abelian group of order 4 and every element of
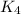 is of order 2 except identity element and generated by 2 elements of order 2 and dihedral group can be also generated by two elements of order 2
is of order 2 except identity element and generated by 2 elements of order 2 and dihedral group can be also generated by two elements of order 2
Hence, <x,y> is isomorphic to
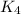 or
or
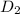 .
.