Question

A man (mass=68 kg) on a parachute is falling at terminal velocity (v=59 m/s)

At which rate do the internal energy of the man and of the air around him increase?

Answer 1

Step-by-step explanation:

It is given that,

Mass of the man, m = 68 kg

Terminal velocity of the man, v = 59 m/s

We need to find the rate at which the internal energy of the man and of the air around him increase. The gravitational potential energy of the man is given by :

`E=mgh`

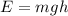
Differentiating equation (1) wrt t as :

`(dE)/(dt)=mg(dh)/(dt)`

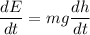
Since,
`v=(dh)/(dt)=59\ m/s`

`(dE)/(dt)=68* 9.8* 59`

`(dE)/(dt)=39317.6\ J/s`

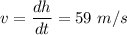
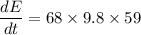
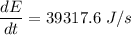
So, the internal energy of the man and the air around him is increasing at the rate of 39317.6 J/s. Hence, this is the required solution.