Question

How many moles of Ni(OH)2 are soluble in 1L of sodium hydroxide (NaOH) when the pH is 12.34?

pKsp of Ni(OH)2 = 15.8

Answer 1

`[Ni^(2+) ]=3.31x10^(-13) M`

Therefore there is
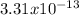`3.31x10^(-13)` moles of
`[Ni^(2+) ]`

in one liter of this solution.

Step-by-step explanation:

This is a problem of common ion effect. In an equilibrium, by the Le Chatelier's principle, when the concentration of a given species rises the equilibrium shifts to the direction that consumes the species that increased in concentration.

Therefore, if a common ion is present in a solubility equilibrium the molar solubility shall decrease.

1) First of all, calculate Ksp and molar solubility in pure solvent

• Ksp

The problem states that pKsp=15.8. The 'p' is the '-log' function, so 'pKsp' expresses '-log(Ksp)'. Isolating for 'Ksp' gives:

`-Log_(10) K_(sp)=15.8`

`Log_(10) K_(sp)=-15.8`

`K_(sp)=10^(-15.8)`

`K_(sp)=1.58x10^(-16)`

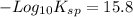
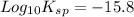
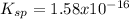
• Molar solubility in pure solvent

`K_(sp)=[Ni^(2+)][OH^(-)]^(2)`

`S=[Ni^(2+)]` and
`[OH^(-)]=2S`, where 'S' stands for molar solubility.

Then Ksp expression can be expressed as:

`K_(sp)=S*(2S)^(2)`

`K_(sp)=4S^(3)`

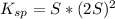
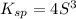
Isolating for 'S' gives us the molar solubility in pure water:

`S=\sqrt[3]{(K_(sp) )/(4) }`

`S=3.4x10^(-6)`

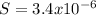
We only calculate the pure solvent molar solubility to compare with the solubility with the common ion and make sure the first is grater, witch confirms the Le Chatelier's principle.

2) Calculate the molar solubility with the common ion

• First we calculate the
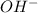  `OH^(-)` concentration from the pH value

In a solution with a pH of 12.34 the pOH is 1.66 (14=pH+pOH)

`-Log_(10) [OH^(-) ]=1.66`

`Log_(10) [OH^(-) ]=-1.66`

`[OH^(-) ]=10^(-1.66)`

`[OH^(-) ]=0.0219`

• Then we input this value in the Ksp expression

`K_(sp)=[Ni^(2+)][OH^(-)]^(2)`

`[Ni^(2+)]=(K_(sp))/([OH^(-)]^(2))`

`[Ni^(2+)]=(1.58x10^(-16))/(0.0219^(2))`

`[Ni^(2+)]=3.31x10^(-13)`

The molar solubility of Ni(OH)2 when there is excess OH- in solution is lower than when the solvent is pure, which indicates that the Le Chatelier's principle has been obeyed.

Answer 2

⇒ 3.312 E-13 mol Ni(OH)2 are soluble in 1 L of solution (NaOH)

Step-by-step explanation:

• Ni(OH)2 ↔ Ni2+ + 2OH-

S S 2S + 0.0218

∴ pKsp Ni(OH)2 = 15.8 = -Log Ksp

⇒ Ksp = 1.585 E-16 = [ Ni2+ ] * [ OH- ]²

• NaOH ↔ Na+ + OH-

∴ pH = 12.34

⇒ pOH = 14- 12.34 = 1.66 = - Log [ OH- ]

⇒ [ OH- ] = 0.0218 M

⇒ Ksp = 1.585 E-16 = S * ( 2S + 0.0218 )²

if we compare the concentration ( 0.0218 ) with the Ksp ( 1.585 E-16 ), then we can neglect the solubility as adding

⇒ 1.585 E-16 = S * ( 0.0218 )²

⇒ 1.585 E-16 = 4.786 E-4 * S

⇒ S = 3.312 E-13 mol/L

∴ soluble moles Ni(OH)2 = 3.312 E-13 mol/L * 1 L Sln = 3.312 E-13 moles

⇒ % S = ( 3.312 E-13 / 0.0218 ) * 100 = 1.513 E-11 %.....we can accept the previous assumption.