Question

A rocket, which is in deep space and initially at rest relative to an inertial reference frame, has a mass of 56.6 × 105 kg, of which 8.50 × 105 kg is fuel. The rocket engine is then fired for 240 s, during which fuel is consumed at the rate of 350 kg/s. The speed of the exhaust products relative to the rocket is 2.38 km/s.

(a) What is the rocket's thrust? After the 240 s firing, what are
(b) the mass and
(c) the speed of the rocket?

Answer 1

b) 5546000 kg

c) 48.42 m/s

Step-by-step explanation:

Mass of fuel = 8.5×10⁵ kg

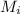`M_i` = Mass of ship = 56.6×10⁵ kg

R = Burn rate = 350 kg/s

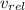`v_(rel)` = Speed of the exhaust products relative to the rocket = 2.37 km/s

Thrust

`T = Rv_(rel)\\\Rightarrow T = 350* 2.38* 10^3\\\Rightarrow T = 833000 N`

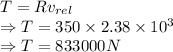
Thrust is 833000 N

Mass of fuel consumed in 240 s

350×240 = 84000 kg

Mass of ship after 240 s

`M_f=M_i-\text{Mass of fuel consumed}=56.6* 10^5-84000 = 5576000\ kg`

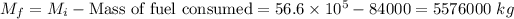
Mass of ship after 240 s is 5576000 kg

Speed of rocket

`v=u+v_(rel)ln(M_i)/(M_f)\\\Rightarrow v=0+2.38* 10^3ln(56.6* 10^5)/(5576000)\\\Rightarrow v=35.58\ m/s`

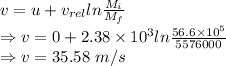
The speed of the rocket after 240 s is 35.58 m/s