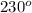Question

A 5.5-µC point charge is located at x = 0.9 m, y = 3.4 m, and a -3.6-µC point charge is located at x = 2.3 m, y = -1.9 m.

(a) Find the magnitude and direction of the electric field at x = -2.9 m, y = 1.2 m.

magnitude kN/C:

direction °:

(b) Find the magnitude and direction of the force on a proton at x = -2.9 m, y = 1.2 m.

magnitude N :

direction ° :

Answer 1

The electric field magnitude= 2.27kN/C direction=
`230^o`

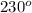
The force is
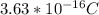`3.63*10^(-16) C` direction=
`230^o`

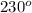
Step-by-step explanation:

Here we have an array of charged points, we have to calculate the net force in the point x=-2.9m and y=1.2m; so we need have to find the distance of all the charged point from this position.

to obtain the distance we have to do this:

`X'=x2-x1 \\Y'=y2-y1\\d=\sqrt{X'^2+Y'^2`

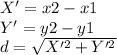
fot the charge of 5.5uC

`X'=0.9-(-2.9)=3.8m\\Y'=3.4-1.2=2.2\\d_(5.5) =√((3.8)^2+(2.2)^2) =4.39m`

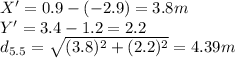
θ
`=tg^(-1) ((2.2)/(3.8) )=30^(o)`

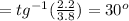
and for the charge of -3.6uC

`X'=2.3-(-2.9)=5.2m\\Y'=-1.9-1.2=-3.1\\d_(3.6) =√((5.2)^2+(-3.1)^2) =6.05m`

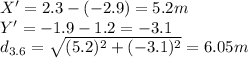
θ
`=tg^(-1) ((3.1)/(5.2) )=30.8^(o)`

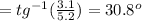
Now that we have the distance and the angle, we can calculate the electric field; ausuming a positive charge:

`E=k*(q)/(r^2)`

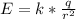
The net force in X direction:

`E_(x) =k*(q)/(r^2)*cos(angle)`

`E_(x) =9*10^(9) ((3.6*10^(-6))/(6.05^2)cos(30.8) -(5.5*10^(-6))/(4.39^2)cos(30))\\E_(x) =-1.46*10^(3)(N)/(C)`

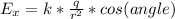
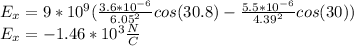
the net force in Y direction:

`E_(y) =9*10^(9) (-(3.6*10^(-6))/(6.05^2)sin(30.8)-(5.5*10^(-6))/(4.39^2)sin(30) )\\E_(y) =-1.74*10^(3)(N)/(C)`

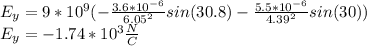
So the magnitud of the electric field is:

`\sqrt{E_(x) ^2+E_(y) ^2} =2.27kN/C`

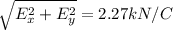
with a direction of:

θ
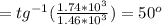`=tg^(-1)((1.74*10^3)/(1.46*10^3) )=50^o`, because is going down and to the left, we have to add 180, so the direction is=
`230^o`

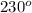
to obtain the force of a proton we only have to multiply the Electric field times the charge of the proton, that is:

`F=E*q\\F=2.27*10^(3)*1.6*10^(-19)\\F=3.63*10^(-16) C`

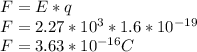
As we calculated the electric field assuming that the charge was a positive, the direction of the force will be the same.
`230^o`