Question

Advanced photodiode detectors have a second light-emitting diode, operating at a wavelength of 2.0 × 10-7 m, to detect even smaller smoke particles from smoldering flames. What is the frequency difference between the two light beams?A) 12.0 × 10^15 HzB) 3.0 × 10^15 HzC) 2.0 × 10^15 HzD) 1.0 × 10^15 Hz

Answer 1

Frequency,
`f=1.5* 10^(15)\ Hz`

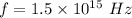
Step-by-step explanation:

It is given that,

Wavelength of the light- emitting diode,
`\lambda=2* 10^(-7)\ m`

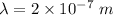
We need to find the frequency difference between the two light beams. It can be calculated using the following relation as :

`c=f* \lambda`

`f=(c)/(\lambda)`

`f=(3* 10^8)/(2* 10^(-7))`

`f=1.5* 10^(15)\ Hz`

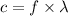
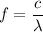
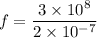
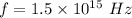
So, the frequency difference between the two light beams is
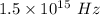`1.5* 10^(15)\ Hz`. Hence, this is the required solution.