Question

Verify which of the following are identities.

Answer 1

My guess would most likely be the first image.

Explanation:

Answer 2

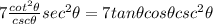`7(cot^(2)\theta )/(csc \theta) sec^(2) \theta=7tan\theta cos\theta csc^(2)\theta` is an identity.

Explanation:

Among the choices, the second expression is an identity, because each part is equivalent to another.

If we develop each part, we will find that they are equivalent

`7(cot^(2)\theta )/(csc \theta) sec^(2) \theta=7tan\theta cos\theta csc^(2)\theta`

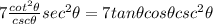
But,

`cot\theta=(cos \theta)/(sin \theta) \implies cot^(2) \theta=(cos^(2) \theta)/(sin^(2) \theta)`

`csc\theta =(1)/(sin \theta) \implies csc^(2) \theta =(1)/(sin^(2) \theta)`

`sec \theta = (1)/( cos \theta)`

`tan\theta = (sin \theta)/(cos \theta)`

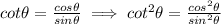
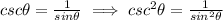
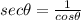
Replacing all these identities, we have

`7(cot^(2)\theta )/(csc \theta) sec^(2) \theta=7tan\theta cos\theta csc^(2)\theta\\((cos^(2) \theta )/(sin^(2) \theta ) )/((1)/(sin \theta) ) (1)/(cos^(2) \theta)=(sin\theta)/(cos\theta) cos \theta (1)/(sin^(2) \theta) \\(cos^(2)\theta sin\theta)/(sin^(2) \theta cos^(2)\theta ) =(1)/(sin\theta) \\(1)/(sin\theta)=(1)/(sin\theta)`

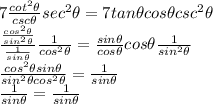
So, as you can see, using the propoer identities, we can demonstrate that the given expression is an identity as such, because it represents an equivalence.

Therefore, the second expression is an identity.