Question

Water standing in the open at 29.2°C evaporates because of the escape of some of the surface molecules. The heat of vaporization (548 cal/g) is approximately equal to εn, where ε is the average energy of the escaping molecules and n is the number of molecules per gram.

(a) Find ε.
(b) What is the ratio of ε to the average kinetic energy of H2O molecules, assuming the latter is related to temperature in the same way as it is for gases?

Answer 1

a) ε = 6.86x
`10^(-20)` J

b) ε/Kavg = 10.98

Step-by-step explanation:

a) The heat of evaporation (Lv) is

Lv = εn

ε = Lv/n

n is the number of molecules in a gram of the substance. The molar mass of water (H2O) is 2x1 g of H + 16 g of O = 18 g/mol.

By the Avogadros' number(NA), we know that 1 mol = 6.02x
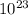`10^(23)` molecules, so n will be:

n = NA/ molar mass

n =
`(6.02x10^(23) )/(18)`

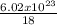
n = 3.34x
`10^(22)` molecules/g

So,

ε =
`(548)/(3.34x10^(22) )`

ε = 1.64x
`10^(-20)` cal

As 1 cal = 4.18 J, ε = 6.86x
`10^(-20)` J

b) For ideal gases, the average of the kinetic energy (the internal energy of the molecules) is given by :

Kavg =
`(3)/(2)`kT

Where Kavg is the average of the kinetic energy, k is the Boltzmann's constant and T is the temperature in Kelvin.

Knowing that k = 1.38x
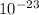`10^(-23)` J/K and T = 29.2ºC + 273 = 302.2 K

Kavg =
`(3)/(2)`x1.38x
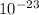`10^(-23)`x302.2

Kavg = 6.25x
`10^(-21)` J

So the ratio of ε to the average kinetic energy of H2O molecules is

ε/Kavg =
`(6.86x10^(-20) )/(6.25x10^(-21) )`

ε/Kavg = 10.98