Question

If gain of the critically damped system is increased, the system will behave as a) Under damped b) Over damped c) Critically damped d) Oscillatory

Answer 1

a) Under damped

Step-by-step explanation:

Given that system is critically damped .And we have to find out the condition when gain is increased.

As we know that damping ratio given as follows

`\zeta =(C)/(C_c)`

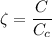
Where C is the damping coefficient and Cc is the critical damping coefficient.

`C_c=2√(mK)`

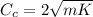
So from above we can say that

`\zeta =(C)/(2√(mK))`

`\zeta \alpha (1)/(\sqrt K)`

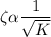
From above relationship we can say when gain (K) is increases then system will become under damped system.