Answer:
Frequency,
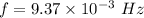
Explanation:
Given that : The wavelength of the wave,

To find : Frequency of a wave
Formula used :
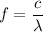
Where c is the speed of light
We know that the relationship between the frequency, wavelength and the speed of light is given by :
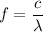
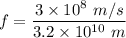
f = 0.009375 Hz
or
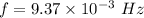
So, the frequency of a wave is
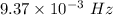 . Hence, this is the required solution.
. Hence, this is the required solution.