Question

An object that is 2 cm tall is 18 cm in front of a converging lens and creates a real image 8 cm beyond the lens. What is the focal length of the lens?

What is the height of the image?

Answer 1

The focal length of the lens is 5.54 cm and the height of the image is -0.89 cm.

Step-by-step explanation:

Given that,

Height of object h = 2 cm

Object distance u= -18 cm

Image distance v= 8 cm

We need to calculate the focal length of the lens

Using formula of lens

`(1)/(f)=(1)/(v)-(1)/(u)`

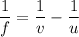
Where, f = focal length

Put the value into the formula

`(1)/(f)=(1)/(8)-(1)/(-18)`

`(1)/(f)=(13)/(72)`

`f=5.54\ cm`

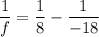
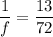
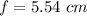
(II). We need to calculate the height of the image

Using formula of magnification

`m =(v)/(u)=(h')/(h)`

`(v)/(u)=(h')/(h)`

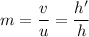
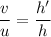
Put the value into the formula

`(8)/(-18)=(h')/(2)`

`h'=(8)/(-18)*2`

`h'=-0.89\ cm`

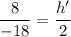
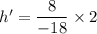
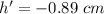
Hence, The focal length of the lens is 5.54 cm and the height of the image is -0.89 cm.