Question

Scientists have investigated how quickly hoverflies start beating their wings when dropped both in complete darkness and in a lighted environment. Starting from rest, the insects were dropped from the top of a 40-cm-tall box. In the light, those flies that began flying 200 ms after being dropped avoided hitting the bottom of the box 80% of the time, while those in the dark avoided hitting only 22% of the time.

A. How far would a fly have fallen in the 200 ms before it began to beat its wings?

B. How long would it take for a fly to hit the bottom if it never began to fly? In seconds.

Answer 1

The distance the fly would have fallen in 200 ms before beating its wings is approximately 0.196 m. If the fly never began to fly, it would take around 0.28 seconds to hit the bottom.

Step-by-step explanation:

A. To calculate the distance the fly would have fallen in the 200 ms before it began to beat its wings, we can use the equation d = 1/2 * g * t², where d is the distance fallen, g is the acceleration due to gravity (9.8 m/s²), and t is the time. Plugging in the values, we get d = 1/2 * 9.8 * (0.2)² = 0.196 m.

B. To calculate how long it would take for a fly to hit the bottom if it never began to fly, we can use the equation t = √(2 * d / g), where t is the time, d is the distance fallen, and g is the acceleration due to gravity. Plugging in the values, we get t = √(2 * 0.4 / 9.8) ≈ 0.28 seconds.

Answer 2

Answers:

A) 0.204 m

B) 0.285 s

Step-by-step explanation:

Answer A:

This described situation is free fall, this means the initial velocity of the fly is zero, and the equation that will be used is:

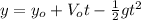`y=y_(o)+V_(o)t-(1)/(2)gt^(2)` (1)

Where:

`y` is the final height of the fly

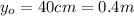`y_(o)=40 cm=0.4 m` is the initial height of the fly

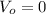`V_(o)=0` is the initial velocity of the fly

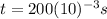`t=200(10)^(-3) s` is the time

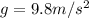`g=9.8 m/s^(2)` is the acceleration due to gravity

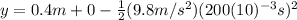`y=0.4 m+0-(1)/(2)(9.8 m/s^(2))(200(10)^(-3) s)^(2)` (2)

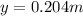`y=0.204 m` (3) This is the distance at which the fly would begin to beat its wings

Answer B:

In this part we will also use equation (1), but we will find the time:

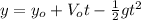`y=y_(o)+V_(o)t-(1)/(2)gt^(2)` (1)

Where:

`y=0` is the final height of the fly

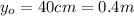`y_(o)=40 cm=0.4 m` is the initial height of the fly

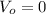`V_(o)=0` is the initial velocity of the fly

`t` is the time we need to find

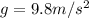`g=9.8 m/s^(2)` is the acceleration due to gravity

`0=0.4 m+0-(1)/(2)(9.8 m/s^(2))t^(2)` (4)

Isolating
`t`:

`t^(2)=((-2)(-0.4 m))/(9.8 m/s^(2))` (5)

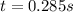`t=0.285 s` (6) This is the time it would take for a fly to hit the bottom of the box