Answer:
The amount of time is 14.44 seconds
Step-by-step explanation:
* Lets explain how to solve the problem
- Dr.Morgan enters the on-ramp to the Merritt Parkway at 15 m/s
∴ His initial velocity u = 15 m/s
- He accelerates at a uniform 3.75 m/s² up the 50 m ramp and for
an additional 160 m on the highway
∴ The acceleration a = 3.75 m/s²
∴ The distance s = 50 + 160 = 210 m
- He hits the brakes, causing him to slow at a rate of 2.50 m/s²
until he reaches the speed limit of 24.6 m/s
∴ The deceleration is 2.50 m/s²
∴ His final velocity v = 24 m/s
- We need to find the time of entire trip
* We have two stage in the problem:
# 1st stage:
- s = 210 m , u = 15 m/s , a = 3.75 m/s²
∵ s = ut + 1/2 at², where s is the distance, u is the initial velocity,
a is the acceleration and t is the time
- Substitute the value of s , u and a in the equation above
∴ 210 = 15t + 1/2 (3.75)t²
∴ 210 = 15t + 1.875t²
- Subtract 210 from both sides
∴ 1.875t² + 15t - 210 = 0
- Solve the equation for t
∴ t = 7.31 seconds
# 2nd stage:
- d = 2.50 m/s² , v = 24.6 m/s
- The initial velocity in this stage is the final velocity of the
1st stage, so lets calculate it
∵ v² = u² + 2as, where v is the final velocity, u is the initial velocity
s is the distance and a is the acceleration
∴ v² = (15)² + 2(3.75)(210) = 1800
∴ v = √1800 = 42.43 m/s
∵ v in the 1st stage is u in the 2nd stage
∴ u = 42.43 m/s
- Now to fine the time of this stage we can use the rule
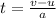
* Remember: d = -a
∴
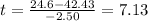seconds
∵ The time of the entire trip is the sum of the time of the 1st stage
and the time of the 2nd stage
∵ t of 1st stage = 7.31 second
∵ t of 2nd stage = 7.13 seconds
∴ The total time = 7.31 + 7.14 = 14.44 seconds
∴ The amount of time is 14.44 seconds