Answer:
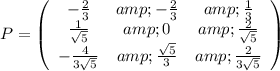
Explanation:
It is a result that a matrix
 is orthogonally diagonalizable if and only if
is orthogonally diagonalizable if and only if
 is a symmetric matrix. According with the data you provided the matrix should be
is a symmetric matrix. According with the data you provided the matrix should be
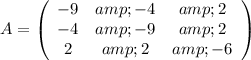
We know that its eigenvalues are
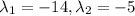 , where
, where
 has multiplicity two.
has multiplicity two.
So if we calculate the corresponding eigenspaces for each eigenvalue we have
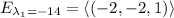 ,
,
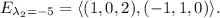 .
.
With this in mind we can form the matrices
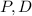 that diagonalizes the matrix
that diagonalizes the matrix
 so.
so.
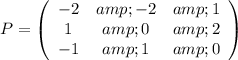
and

Observe that the rows of
 are the eigenvectors corresponding to the eigen values.
are the eigenvectors corresponding to the eigen values.
Now you only need to normalize each row of
 dividing by its norm, as a row vector.
dividing by its norm, as a row vector.
The matrix you have to obtain is the matrix shown below