Answer:
Wavelength is 0.33 nm for n=1, 1.32 nm for n=4, and 3.3 nm for n=10.
Step-by-step explanation:
The velocity of the electron in the nth level of hydrogen atom is,
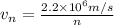
Now the de Broglie wavelength can be calculated as,
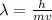
For n=1 the wavelength is,
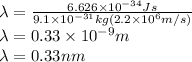
Therefore wavelength for n=1 orbit is 0.33 nm.
For n=4 the wavelength is,
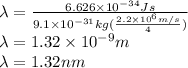
Therefore wavelength for n=4 orbit is 1.32 nm.
For n=4 the wavelength is,
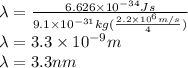
Therefore wavelength for n=10 orbit is 3.3 nm.