Question

In a laboratory population of Drosophila, all the males are XsY. Among the females, 15% are XiXi, 50% are XiXs, and 35% are XsXs. Assuming random mating, what proportion of male flies in the next generation will be XiY?

Answer 1

20 % from the next generation will be male XiY

Explanation:

females have are XX always and males are XY, so when cross a woman an a man the probability of have a male is 50 %

XX - XY

⇒XX

⇒XY

⇒XX

⇒XY

P (female) =
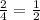`(2)/(4) =(1)/(2)` = 0.5 = 50 %

P (male) =
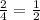`(2)/(4) =(1)/(2)` = 0.5 = 50 %

Then the probability oh have a male XiY is dependent first oh have a male and second that the male will be XiY

The probability of a dependent probability is the product of the probabilities

P (XiY) = P (male) * P (male wit the character Xi)

P (male wit the character Xi) = P (of be XiY from the amount of males from the cross XiXi with XsY) * P (XiXi) + P (of be XiY from the amount of males from the cross XiXs with XsY) * P (XiXs) + P (of be XiY from the amount of males from the cross XsXs with XsY) * P (XsXs)

1. XiXi - XsY

⇒ XiXs (female)

⇒XiXs (female)

⇒XiY (male)

⇒XiY (male)

From the 2 male, both can be XiY

P (of be XiY from the amount of males from the cross XiXi with XsY) =
`(2)/(2) =1`

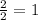
2. XiXs - XsY

⇒ XiXs (female)

⇒XsXs (female)

⇒XiY (male)

⇒XsY (male)

From the 2 male, one can be XiY

P (of be XiY from the amount of males from the cross XiXs with XsY) =
`(1)/(2)`

3. XsXs - XsY

⇒ XsXs (female)

⇒XsXs (female)

⇒XsY (male)

⇒XsY (male)

From the 2 male,any of them can be XiY

P (of be XiY from the amount of males from the cross XsXs with XsY) =
`(0)/(2) =0`

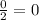
P (male wit the character Xi) = P (of be XiY from the amount of males from the cross XiXi with XsY) * P (XiXi) + P (of be XiY from the amount of males from the cross XiXs with XsY) * P (XiXs) + P (of be XiY from the amount of males from the cross XsXs with XsY) * P (XsXs)

P (of be XiY from the amount of males from the cross XiXi with XsY) = 1

P (of be XiY from the amount of males from the cross XiXs with XsY) =
`(1)/(2)`

P (of be XiY from the amount of males from the cross XsXs with XsY) = 0

P (male wit the character Xi) =
`1*(15)/(100) +(1)/(2) *(50)/(100) +0 * (35)/(100)`=
`(40)/(100)=(2)/(5)`

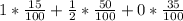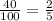
P (XiY) = P (male) * P (male wit the character Xi)

P(XiY) =
`(1)/(2) *(2)/(5) =(1)/(5) = 0.2`

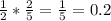
20 % from the next generation will be male XiY