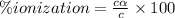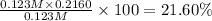Answer:
21.60% is the percent ionization of a 0.123 M solution of this acid.
Step-by-step explanation:
The equilibrium reaction for dissociation of weak acidis,
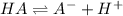
initially conc. c 0 0
At eqm.
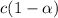
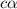
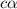
Concentration of the weak acid (c) = 0.123 M
Acid dissociation constant =
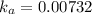
Degree of ionization of weak acid =

An expression of dissociation constant is given as:
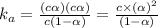
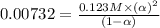
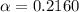
Percent ionization of weak acid: