Answer: 99.51%
Explanation:
Given : A survey found that women's heights are normally distributed.
Population mean :
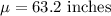
Standard deviation:
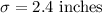
Minimum height = 4ft. 9 in.=
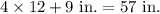
Maximum height = 6ft. 2 in.=
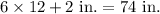
Let x be the random variable that represent the women's height.
z-score :

For x=57, we have
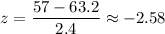
For x=74, we have
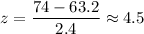
Now, by using the standard normal distribution table, we have
The probability of women meeting the height requirement :-
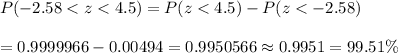
Hence, the percentage of women meeting the height requirement = 99.51%