Question

An artery is constricted at one location to 1/2 its normal cross-sectional area. How does the speed of blood past the constriction compare to the speed of blood flow in the rest of the artery? (Note: Assume ideal fluid flow.)

Answer 1

Speed of blood past the constriction becomes two times the speed of blood flow in the rest of the artery.

Step-by-step explanation:

For an ideal fluid flow condition, the equation of continuity is applicable which means that the flow of any fluid at a given point of time at two different cross section remains same at constant density

Thus,

`A_1V_1= A_2V_2`

`A_1= A\\and\\A_2= (A)/(2)`

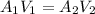
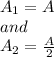
Substituting the given values in above equation, we get -

`A*V_1= (A)/(2) * V_2\\V_1= (V_2)/(2) \\\\V_2 = 2V_1`

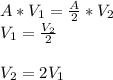
Thus, speed of blood past the constriction becomes two times the speed of blood flow in the rest of the artery.