Question

A rock falls from rest a vertical distance of 0.72 meters to the surface of a planet in 0.63 seconds. The magnitude of the acceleration due to gravity on the planet ?

Answer 1

3.63 meter/sec²

Explanation:

If a rock fall from a height h, then

`h=ut+(1)/(2)gt^2`

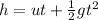
Where g is the acceleration due to gravity, u is initial velocity and t is time in seconds in which the rock reaches the surface.

It is given that a rock falls from rest a vertical distance of 0.72 meters to the surface of a planet in 0.63 seconds.

h = 0.72 meters

u = 0

t = 0.63 seconds

Substitute the given values in the above formula to find the value of g.

`0.72 = (0) * (0.63) +  (1)/(2)g(0.63)^2`

`0.72 = (1)/(2)g(0.63)^2`

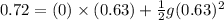
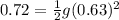
Multiply both sides by 2.

`1.44= 0.3969g`

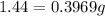
Divide both sides by 0.3969.

`(1.44)/(0.3969)=g`

`g\approx 3.63`

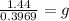
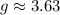
Therefore, the magnitude of the acceleration due to gravity on the planet is 3.63 meter/sec².

Answer 2

3.63 meter/sec²

Explanation:

When a rock fall from a height h with initial velocity u and the rock reaches the surface in t seconds the expression that represents this is

h = 4t +
`(1)/(2)` gt²

Where g is the acceleration due to gravity

Here h = 0.72 meters

u = 0

t = 0.63 seconds

from the given formula

0.72 = 0 ×(0.63) +
`(1)/(2)` g(0.63)²

0.72 =
`(1)/(2)` g(0.63)²

g =
`(2*0.72)/((0.63)^2)`

= 3.63 meter/sec²