Question

A system that has 100,000 molecules at energy level 1; 10,000 molecules at energy level 2, and 1000 molecules at energy level 3. What is the entropy of the system?

Answer 1

`5.31* 10^(-19)`

Step-by-step explanation:

Entropy of the system,
`(S) = - k_(B) lnW`

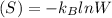
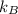`k_(B)` is Boltzmann constant, W is the number of microstates

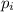`p_(i)` is the probability of a molecule in a given energy level.
`p_(i) =(N_(i) )/(N)`

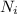`{N_(i) }` = number of molecules in a energy state, N = total number of molecules

And,

`ln W = - N \sum p_(i) lnp_(i)`

In the given problem

`N = 100000+10000+1000 = 111000`

`p_(1)  = 100000/111000 = 0.9009`

`p_(2) = 10000/111000 = 0.09009`

`p_(3) = 1000/111000 = 0.009009`

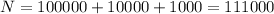
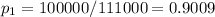
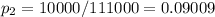
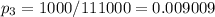
then,

`S = - N k_(B) [p_(1) lnp_(1) + p_(2)lnp_(2) + p_(2)lnp_(2)]`

Therefore,

`S = - Nk_(B) [ 0.9009ln0.9009 + 0.09009ln0.09009 + 0.009009ln0.009]\\S== -111000* 1.38*10^(-23)[ - 0.9009* 0.1 - 0.09009* 2.41 - 0.009009* 4.71]\\S= 111* 1.38* 10^(-20) [ 0.09009 + 0.217+0.04243]\\S= 151.8* 10^(-20)* 0.34952\\S=53.06* 10^(-20) JK^(-1) \\S=5.31* 10^(-19) JK^(-1)`

Therefore entropy of the system is
`5.31* 10^(-19)`