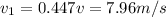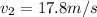Question

One car has two and a half times the mass of a second car, but only half as much kinetic energy. When both cars increase their speed by 9.0 m/s, they then have the same kinetic energy. What were the original speeds of the two cars

Answer 1

`v_1 = 7.96 m/s`

`v_2 = 17.8 m/s`

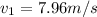
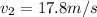
Step-by-step explanation:

Let the mass of the other car is "m" and its kinetic energy is

`K = (1)/(2)mv^2`

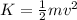
now the mass of the first car is two and half times and its kinetic energy is half that of other car

so we will have

`(1)/(2)(2.5m)v_1^2 = (1)/(2)((1)/(2)mv^2)`

`2.5 v_1^2 = 0.5 v^2`

`v_1 = 0.447 v`

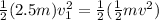
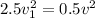
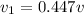
now speed of both cars is increased by value of 9 m/s

so now we will have same kinetic energy for both cars

`(1)/(2)(2.5 m)(0.447v + 9)^2 = (1)/(2)m(v + 9)^2`

`2.5(0.447 v + 9)^2 = (v + 9)^2`

`1.58(0.447v + 9) = v + 9`

`0.293v = 5.22`

`v = 17.8 m/s`

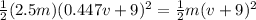
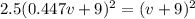
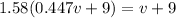
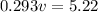
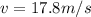
so speed of first car is

`v_1 = 0.447 v = 7.96 m/s`

`v_2 = 17.8 m/s`