Question

You're in a car that gets 28 miles per gallon of gas, driving it at a constant speed. If you took the gas from the car tank, and instead filled a long cylinder or hose alongside the car's path, what would the diameter of the hose need to be?

Answer 1

The diameter of the hose is 0.326 mm.

Step-by-step explanation:

Given that,

Speed of car = 28 miles/galllon

We need to calculate the radius

The rate of flow of fluid is from the equation of continuity

`(V)/(t)=Av`

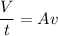
Where, A = area of cross sectional

`(V)/(t)=\pi r^2v`

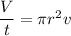
We know that,

The velocity is the ratio of displacement of gas per unit time.

`(V)/(t)=\pi r^(x)/(t)`

`(V)/(x)=\pi r^2`

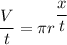
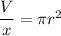
Put the value into the formula

`(0.00378541)/(28*1609.34)=\pi r^2`

`r=\sqrt{(0.00378541)/(28*1609.34*\pi)}`

`r=1.63*10^(-4)\ m`

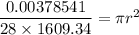
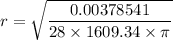
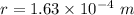
We need to calculate the diameter of the hose

`d = 2r`

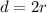
Put the value of r

`d=2*1.63*10^(-4)`

`d=0.326\ mm`

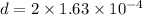
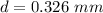
Hence, The diameter of the hose is 0.326 mm.