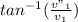Answer:
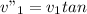 Θ
Θ
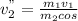 Θ
Θ
Θ =
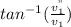
Step-by-step explanation:
Applying the law of conservation of momentum, we have:
Δ
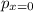
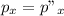
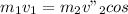 Θ (Equation 1)
Θ (Equation 1)
Δ
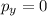
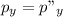
 Θ (Equation 2)
Θ (Equation 2)
From Equation 1:
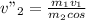 Θ
Θ
From Equation 2:
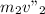 sinΘ =
sinΘ =
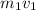
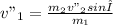
Replacing Equation 3 in Equation 4:
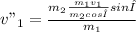
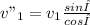
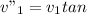 Θ (Equation 5)
Θ (Equation 5)
And we found Θ from the Equation 5:
tanΘ=
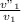
Θ=